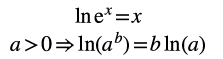Logarithme et exponentielle ont révolutionné les mathématiques dans les siècles précédents, car le logarithme a permis les tables à calcul et l’exponentielle est au cœur d’à peu près toute l’analyse. Ces deux fonctions sont largement étudiées en première et terminale spécialité maths, elles doivent être maîtrisées sur le bout des doigts, mais c’est surtout par la pratique qu’on en acquiert l’aisance. Il convient donc d’avoir un enseignant qui détecte précisément quels seraient chez vous les points à renforcer : compréhension algébrique de ces deux fonctions ? étude des variations de fonctions s’appuyant sur elles ?
Souvent on voit des élèves qui ne voient pas le lien entre l’écriture classique 3^n et l’écriture qu’ils découvrent : e^x. Ou bien, aussi, des élèves à qui on présente l’exponentielle comme l’unique fonction étant elle-même sa dérivée avec f(0)=1 : ces élèves, par la suite, se demandent (question fréquente) si l’exponentielle est une fonction qui « existe vraiment ». Le calcul numérique approché étant « mal vu » au lycée, certains ont des idées très floues quant à l’approximation de e (2.7 est déjà une bonne chose) ce qui les conduit à ne pas voir quand leurs résultats sont abberrants.
Ces deux fonctions permettent de toutes manières de réviser tout ce qui a été appris auparavant : (in)équations ; variations ; convexité ; problèmes avec les tangentes ; modélisation de problèmes concrets. Il vous faut donc une grande quantité de travail, mais de préférence guidée en fonction de vos forces et de vos faiblesses, et il faut commencer assez tôt dans l’année de terminale à acquérir des bases solides sur ces deux thèmes.
L’exponentielle est incontournable : oscillations amorties ; courbe en cloche ; lien avec les équa diff d’ordre 1 (les seules au programme de maths) ; généralisation de a^b. Et le logarithme permet tant de résultats : résolution des équations où x est en exposant pour ne citer que celui-ci. Enfin, La méthode de Briggs a pu constituer des sujets d’oraux que nous avons suggéré à certains étudiants pourle grand oral.